多臂老虎机:随机老虎机的概念、非结构化老虎机、环境类、Bernoulli 老虎机的代码实现
本文先介绍多臂老虎机的符号规范与基本定义,将其建模为含动作集、奖励集与概率分布的三元组,说明其在推荐、广告、投资等领域的应用。接着区分非结构化与结构化老虎机,定义伪遗憾、期望遗憾与遗憾界,指出探索‑利用权衡是核心问题。文末给出相关引理证明,并提供 Bernoulli 老虎机的 Python 实现与 Follow‑The‑Leader 算法示例,通过实验说明该算法遗憾呈线性增长,为后续更优算法作了铺垫。
符号说明
- 大写表示随机变量,例如时间 $t$ 时刻使用的手臂 $A_{t}$ ;
- 小写表示确定的常数,例如 $a_{t}$ 表示时间 $t$ 的时候随机变量 $A_{t}$ 的具体取值.
随机老虎机的基本定义
多臂老虎机简介
多臂老虎机问题通过一个假想的赌博场景定义:假设有 $k$ 台老虎机 (slot machines 或 One-armed bandits),每台老虎机有一个手臂,拉动老虎机的手臂,老虎机会按照一个概率分布随机吐出一些奖币。每一台老虎机的奖币分布不同。假设玩老虎机的轮数事先确定。玩家如果知道每一台老虎机的奖币分布,那么一定会选择获得奖币数的期望值最大的老虎机去玩,最终赢得最多的奖币。但实际情况是,玩家对老虎机的奖币分布一无所知, 需要在玩的过程中进行估计。
多臂老虎机表示一类通用的决策和学习问题,玩家代表智能体,老虎机代表环境。有多个选项,每一个选项的收益未知,智能体与环境交互,目标是依次选择一个选项,最大化获得的总体收益。新闻推荐、在线广告、金融投资、医学治疗等许多问题都可以看作具体的应用:
- 在新闻推荐中,推荐系统是智能体,用户群体是环境,文章是手臂,用户的点击是奖励。
- 在在线广告中,广告系统是智能体,消费者群体是环境,广告是手臂,消费者的点击是奖励;
- 在金融投资中,投资决策系统是智能体,金融市场是环境,投资项目是手臂,投资的回报是奖励;
- 在医学治疗中,医疗决策系统是智能体,病人群体是环境,治疗方法是手臂,治疗的效果是奖励。
随机老虎机的定义
下面是随机老虎机的定义.
定义:随机老虎机
随机老虎机的模型由三元组 $\left\langle \mathcal{A}, \mathbb{R}, \mathbb{P} \right\rangle$ 组成,
- 手臂或动作的有限集合 $\mathcal{A}$ :$a\in \mathcal{A}$ ,$k = |\mathcal{A}|$ .
- 奖励或奖币的集合 $\mathbb{R}$ ;$x\in \mathbb{R}$ ,奖励 $x$ 是一个实数值,有时为了方便,认为奖励是有界的,如设 $x\in [0,1]$ .
奖励的概率分布 $\mathbb{P}(x\mid a)$ :$\mathcal{A}\in \mathbb{R}\to [0,1], a\in \mathcal{A}, x\in \mathbb{R}$ ,选择手臂 $a$ 得到奖励 $x$ 的概率是 $\mathbb{P}(x\mid a)$ ,为方便,我们用 $\mathbb{P}_{a}$ 来表示手臂 $a$ 后面的具体分布. 此外,还用
$$ v = \left\lbrace \mathbb{P}_{a}, a\in \mathcal{A} \right\rbrace $$
来表示所有手臂背后概率分布的集合,因此也可直接用 $v$ 来指代一个随机老虎机.
对于一个老虎机,它的分布是确定的,因此可以计算一个手臂 $a$ 的期望奖励(手臂价值):
$$ Q(a) = \mathbb{E}[X\mid a] $$
这里 $X$ 表示奖励随机变量,最优期望奖励则是
$$ Q_{*} = \max_{a} Q(a) $$
最优手臂是
$$ a_{*} = \arg\max_{a} Q(a) $$
Agent 已知的是所有可能的手臂(动作集合已知),但是不知道每个手臂的概率分布,Agent 和老虎机进行 $T$ 轮交互,在第 $t$ 轮交互当中,智能体选择一个手臂 $A_{t}$ ,老虎机从对应的奖励分布随机生成一个奖励 $R_{t}$ .
一个重要假设就是:选择同一个手臂得到的奖励数据是独立同分布的. 因此我们也可以应用估计理论.
$T$ 轮交互当中的总体回报为
$$ G = \sum\limits_{t=1}^{T} X_{t} $$
$X_{t}$ 表示 $t$ 时刻的奖励随机变量,Agent 的目标是最大化总体奖励 $G$ ,以上问题称为多臂老虎机问题 (MAB).
例 1:二臂 Bernoulli 老虎机
设 $\mathcal{A} = \left\lbrace a_{1},a_{2} \right\rbrace$ 为二臂老虎机,其中 $a_{1}$ 对应的老虎机概率分布为 $B(1,0.3)$ ,$a_{2}$ 对应为 $B(1,0.5)$ .
对于这个例子,最优手臂肯定是 $a_{2}$ ,因为其期望更大. 所以简单来说,多臂老虎机就是选取均值更大的分布,不过分布参数要通过 agent 探索来进行估计. $\square$
例 2:决策问题建模为多臂老虎机
假设你一年经常患感冒,那么每次感冒时,有三种药物可供挑选:板蓝根、蒲地蓝、感冒灵,而你不知道他们三者哪个更适合你,因此可以建模为一个三臂老虎机,然后每次感冒时,都尝试其中一个药品来看看效果.这种建模方式的好处在于,身体状况可能每次不太一样,可以理解成药效是受随机性影响的. 因此随机老虎机是很合适的.
需要注意的是,尽管我们用均值来判断手臂的价值,但是在实际的决策问题当中,这种价值可能有失偏颇,假设我们此时有个两臂的老虎机,对应的分布分别为
$$ N(1, 1), \quad N(1,100) $$
也就是两个仅仅在方差上有差别的高斯分布(正态分布),此时到底应该判断哪个手臂更好?这取决于场景. 很多情况下,我们是厌恶风险的,此时应该称 Agent 是 risk sensitive 的(风险敏感).
关于这一类的问题,这里给出一个参考文献. 1 我也可能在之后学习这一部分的内容.
环境类 (Environment Class)
为方便刻画不同类型的老虎机,随机老虎机实际上还有一些分类,这种分类是在我们对老虎机有些先验知识的时候采用的. 例如:如果我们在医药上给病人服药,奖励只有 0 (无效)和 1 (有效)的分别,那么老虎机实际上考虑 Bernoulli 老虎机比较好.
定义:环境类
通过定义一个随机老虎机集合 $\mathcal{E}$ ,通过 $v\in \mathcal{E}$ 可以刻画一批特殊的老虎机,我们称 $\mathcal{E}$ 为环境类 (environment class).
通过对 $\mathcal{E}$ 的限定,主要可以分为两类:结构化和非结构化的老虎机. 这个部分主要来自于 2
的说明.
非结构化老虎机 (Unstructured Bandits)
定义:非结构化环境类
如果 $\mathcal{A}$ 是有限的,且存在概率分布集合 $\mathcal{M}_{a}, \forall a\in \mathcal{A}$ ,对环境类 $\mathcal{E}$ 都有
$$ \mathcal{E} = \left\lbrace v = (\mathbb{P}_{a} : a\in \mathcal{A}): \mathbb{P}_{a} \in \mathcal{M}_{a}, \forall a\in \mathcal{A} \right\rbrace $$
则称 $\mathcal{E}$ 是非结构化的. 此外,非结构化的环境类可以表达为乘积空间:
$$ \mathcal{E} = \times_{a\in \mathcal{A}} \mathcal{M}_{a} $$
非结构化的环境类实际上就是对老虎机的分布做了个限定,上述的定义看上去很抽象,这是因为它就是要刻画最广泛的一类老虎机:
- 不假设奖励分布来自于某个参数族;
- 不假设臂之间有顺序、有相似度、有特征;(这个很重要,因为非结构化的老虎机可以表达为整个乘积空间)
- 不假设均值有某种结构(比如线性模型、低维)
也就是只知道有 $k$ 个臂,每个臂有固定但未知的奖励分布,除此之外什么都不知道.
例 3:Bernoulli 老虎机
设 $\mathcal{M}_{a} \equiv \left\lbrace B(\mu), \mu \in [0,1] \right\rbrace$ ,那么此时对于非结构化环境类 $\mathcal{E}$ :
$$ \mathcal{E} = \left\lbrace (B(\mu_{1}), B(\mu_{2}), \cdots, B(\mu_{k})), \mu_{a}\in [0,1], \forall a\in \mathcal{A} \right\rbrace $$
则为 Bernoulli 老虎机.
说人话就是每个手臂背后都是 Bernoulli 分布,参数根据手臂编号变化. 这种环境类我们记为 $\mathcal{E}_{B}^{k}$ ,表示 $k$ 臂的 Bernoulli 老虎机集合.
同理还有均匀分布的 $\mathcal{E}_{U}^{k}$ 以及正态分布的 $\mathcal{E}_{N}^{k}$ .
如果有未定的参数,例如 Bernoulli 老虎机类当中的均值参数,则称为参数老虎机环境类,反之则是非参老虎机环境类. (一个分类而已,不算太重要)
结构化老虎机 (Structured Bandits)
任何不是非结构化老虎机的老虎机统称为结构化老虎机. 这里可就百花齐放了,而且建模方式千奇百怪,这也是为何老虎机模型应用广泛.
例 4:手臂间存在关系的结构化老虎机
令 $\mathcal{A} = \left\lbrace 1,2 \right\rbrace$ 且 $\mathcal{E} = \left\lbrace (\mathcal{B}(\theta), \mathcal{B}(1-\theta)):\,\theta\in [0,1] \right\rbrace$ .
为什么它是结构化的呢?因为参数的共享导致维度降低了,不再能表达为整个乘积空间了,我们只需要学一个手臂就能学整个老虎机.
这也可以看出,非结构化和结构化的老虎机学习难度是不同的.
例 5:随机线性老虎机
令 $\mathcal{A}\subset \mathbb{R}^{d}$ 且 $\theta\in \mathbb{R}^{d}$ ,且
$$ v_{\theta} = (N(\left\langle a, \theta \right\rangle, 1): a\in \mathcal{A}), \quad \mathcal{E} = \left\lbrace v_{\theta}: \theta\in \mathbb{R}^{d} \right\rbrace $$
这里也是类似的,所有的手臂共享了参数 $\theta$ ,因此随机线性老虎机是结构化的老虎机.
遗憾 (regrets)
(伪)遗憾
尽管我们已经知道目标是最大化回报 $G$ ,但是这个问题并不能算是一个严格的优化问题,原因有几个:
- $R_{t}$ 的取值是随机的,因此尽管我们可能选中的比较好的手臂,我们也不能保证 $G$ 就是最大的.
- 很多场景下 $T$ 我们是不一定会固定的,假设我们真的在一个赌场里面拉老虎机试图得到最大值,我们的成本浮动会导致我们可能不得不提前停下来.
正因为如此,我们需要稍微再设计一下优化目标.
定义:遗憾
对于随机老虎机 $v$ ,如果智能体采用策略 $\pi$ 使用该老虎机,则在 $T$ 轮交互中的遗憾 (regret) 定义为:$$ R_{T}(\pi,v) = T\cdot Q_{*} - \sum\limits_{t=1}^{T} Q(A_{t}) $$
其中 $Q_{*} = \arg\max_{a\in \mathcal{A}} Q(a)$ 是最优期望奖励,$Q(A_{t})$ 是手臂 $A_{t}$ 的期望奖励,那么在 $T$ 轮交互中的期望遗憾是:
$$ \mathbb{E}[R_{T}(\pi,v)] = \mathbb{E}\left[T \cdot Q_{*} - \sum\limits_{t=1}^{T} Q(A_{t}) \right] $$
这里的期望是对 $A_{t}$ 求期望.
遗憾是 agent 的方案和“每次都拉动最优手臂”这个最优方案的距离. 注意这里期望遗憾的存在是因为 $A_{t}$ 是随机变量,所以 $Q(A_{t})$ 也应该认为是随机变量.
也有一些材料将上述的遗憾称为伪遗憾 (psedo-regret) ,而期望遗憾称之为遗憾. 为减少误导,我会在之后使用伪遗憾和期望遗憾分别指代.
对于期望遗憾,我们有如下的性质:
引理:期望遗憾的基本性质
令 $v$ 为随机老虎机,则
- 无论使用什么策略 $\pi$ ,期望奖励一定非负;
- 如果策略 $\pi$ 对任意 $t$ 挑选 $A_{t}$ 时,每次都实现最优期望奖励,则期望遗憾为 $0$ .
- 如果存在策略 $\pi$ 使得期望奖励 $\mathbb{E}[R_{T}(\pi,v)]=0$ ,那么对于任意 $t=1,2,\cdots, T$ ,都有 $\mathbb{P}(Q(A_{t}) = Q^{*})=1$ .
证明见后面的习题. $\square$
遗憾界 (regret bound)
我们从引理可以知道,期望遗憾要达到 $0$ ,在有限的时间内,除非智能体完全了解背后的分布,或者说每次都选到最优臂,这在通常的应用当中是不可能的.
那么不妨退而求其次,我们将时间放到无穷,我们希望:
$$ \forall v\in \mathcal{E}, \quad \lim_{T\to \infty}\dfrac{\mathbb{E}[R_{T}(v, \pi)]}{T} =0 $$
这个极限式是什么含义呢?它表示在给定无穷时间后,智能体几乎一直选择最优臂. 这就要求智能体能在不断的实践当中学习到真正的最优.
换言之,其实就是要证明:存在 $C>0$ 以及 $p<1$ 使得
$$ \forall v\in \mathcal{E}, \quad {\mathbb{E}[R_{T}(v, \pi)]} \leqslant C n^{p} $$
我们往往用 $O(n^{p})$ 来表示这个阶,这个也称之为遗憾界,它是老虎机算法的研究重点,遗憾界越紧,算法收敛效果越好.
探索-利用权衡 (exploration and exploitation trade-off)
对于 Agent 而言,最大的难题无疑是:它是坚持目前最好的手臂,还是探索更好的手臂?这个也叫做探索-利用权衡. 之后介绍的算法都将会是为了这个问题做出改进.
对于接下来的问题,我们讨论算法时,选择 $k$ 臂老虎机进行讨论,同时奖励我们也直接设定为 $[0,1]$ 的.
习题与代码实践
引理的证明
引理:期望遗憾的基本性质
令 $v$ 为随机老虎机,则
- 无论使用什么策略 $\pi$ ,期望奖励一定非负;
- 如果策略 $\pi$ 对任意 $t$ 挑选 $A_{t}$ 时,每次都实现最优期望奖励,则期望遗憾为 $0$ .
- 如果存在策略 $\pi$ 使得期望奖励 $\mathbb{E}[R_{T}(\pi,v)]=0$ ,那么对于任意 $t=1,2,\cdots, T$ ,都有 $\mathbb{P}(Q(A_{t}) = Q^{*})=1$ .
(1) 因为伪遗憾满足:
$$ R_{T}(\pi,v) = T\cdot Q_{*} - \sum\limits_{t=1}^{T} Q(A_{t}) \geqslant T\cdot Q_{*} - \sum\limits_{t=1}^{T} Q_{*} = 0 $$
因此期望遗憾也是非负的.
(2) 这个也是显然的,此时的 $Q(A_{t}) = Q^{*}$ ,按照定义即得结论.
(3) 若不然,则 $\mathbb{P}(Q(A_{t}) < Q^{*}) = \varepsilon > 0$ ,设 $\mathcal{A}^{*} \subset \mathcal{A}$ 是能使得 $Q(a) = Q^{*}$ 的所有手臂 $a$ 集合,如果 $\mathcal{A}^{*} = \mathcal{A}$ ,那么结论已然成立,否则考虑从 $\mathcal{A}\setminus \mathcal{A}^{*}$ 当中选择使得 $Q(a)$ 最大的手臂记为 $a^{*}$ ,因此有
$$ \mathbb{E}[R_{T}(\pi, v)] = \sum\limits_{t=1}^{T} \mathbb{E}[Q^{*} - Q(A_{t})] \geqslant T \varepsilon (Q^{*} - Q(a^{*})) >0 $$
因此出现矛盾,从而结论成立. $\square$
代码实践:Bernoulli 老虎机
我们引入下面的模板来实现 Bernoulli 老虎机.
import numpy as np
class BernoulliBandit:
# accepts a list of K >= 2 floats, each lying in [0,1]
def __init__(self , means):
pass
# Function should return the number of arms
def K(self):
pass
# Accepts a parameter 0 <= a <= K-1 and returns the
# realisation of random variable X with P(X = 1) being
# the mean of the (a+1)th arm.
def pull(self , a):
pass
# Returns the regret incurred so far.
def regret(self):
pass有意向练习的读者可用上述的空模板,也可直接运行下面的实现.
class BernoulliBandit:
# accepts a list of K >= 2 floats, each lying in [0,1]
def __init__(self , means: Union[list, np.ndarray]):
# 确认输入合法
try:
l = len(means)
except Exception:
print("Invalid input.")
# 确认输入在 0-1
if np.min(means) < 0 or np.max(means) > 1:
warnings.warn("[WARN] Your Bernoulli bandit has means out of range [0,1]. It will be transformed into [0,1] automatically.")
means = np.abs(means - np.max(means)) / (np.max(means) - np.min(means))
self.means = np.asarray(means)
self.K_ = l
self.regret_ = 0
self.optimal_mean = np.max(means)
# Function should return the number of arms
@property
def K(self):
return self.K_
# Accepts a parameter 0 <= a <= K-1 and returns the
# realisation of random variable X with P(X = 1) being
# the mean of the (a+1)th arm.
def pull(self , a):
assert (a >= 0 and a < self.K_), "Please pull a valid arm: 0, 1, 2, ..., (K-1)"
reward = np.random.binomial(n=1, p=self.means[a])
self.regret_ += self.optimal_mean - self.means[a]
return reward
# Returns the regret incurred so far.
@property
def regret(self):
return self.regret_
到这里,我们再用一个简单的算法,来看看效果,我们将每个手臂试一遍,这一遍当中表现最好的手臂我们就认为是最优然后一直使用,看看遗憾会如何增长. 为方便绘图,我们返回所有时刻的遗憾:
def follow_the_leader(bandit , n: int):
scores = []
regrets = []
for i in range(min([bandit.K, n])):
scores.append(bandit.pull(i))
regrets.append(bandit.regret)
optimal_arms = np.where(scores == np.max(scores))[0]
for _ in range(n - bandit.K):
arm = np.random.choice(optimal_arms)
bandit.pull(arm)
regrets.append(bandit.regret)
return np.array(regrets)利用 Bernoulli 老虎机绘图 100 轮的结果:
np.random.seed(0)
n=500
bandit = BernoulliBandit(np.array([0.4, 0.6, 0.1, 0.2, 0.75, 0.5, 0.8]))
regrets = follow_the_leader(bandit, n=n)
plt.plot(list(range(n)), regrets)
plt.title("Bernoulli bandit with follow the leader: regret plot")
plt.show()因此可以绘图如下所示:
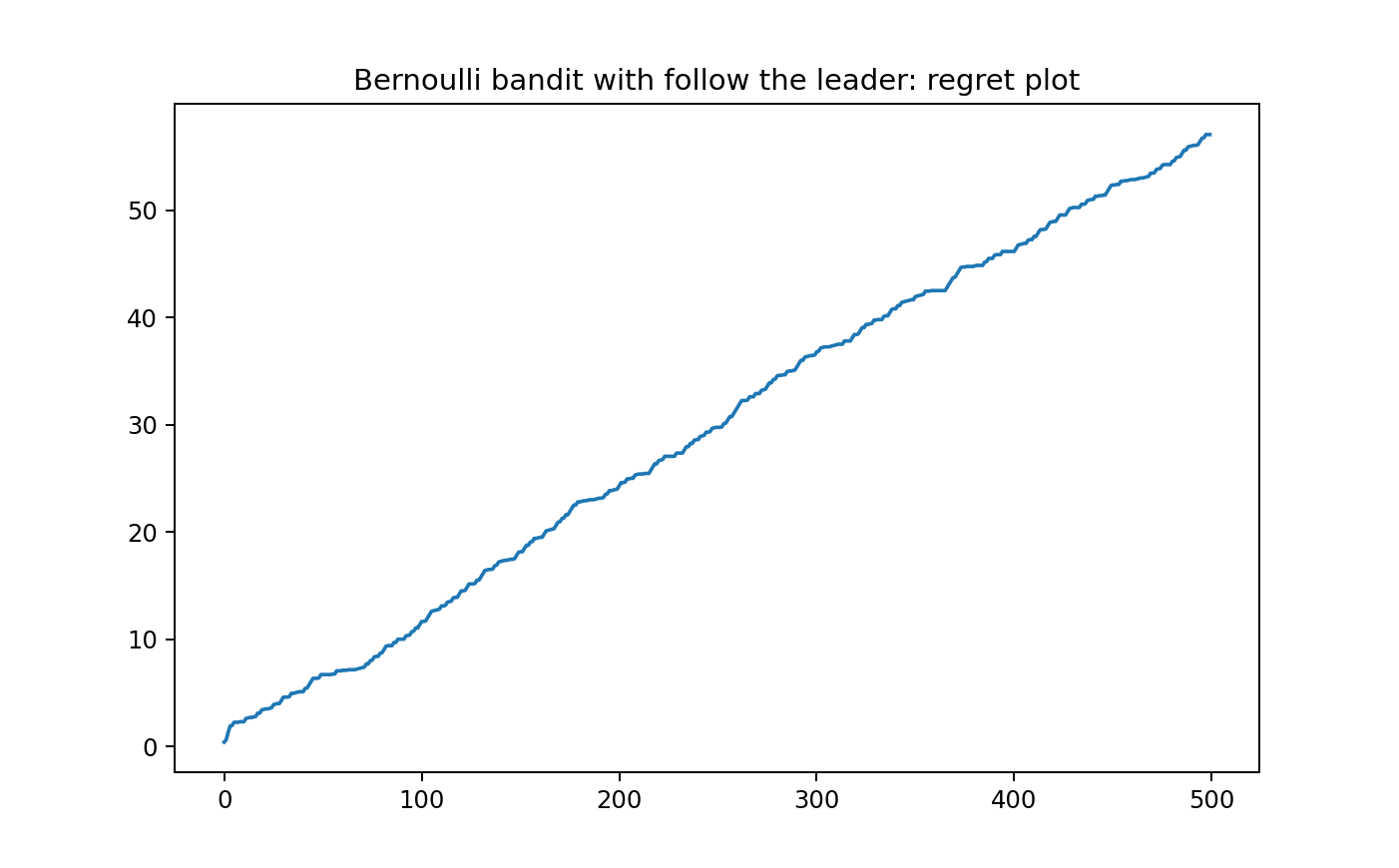
可以看到算法的表现其实并不好,遗憾呈现的是线性的状态,在之后,我们将会引入一些能实现次线性遗憾界的算法.
参考文献
- V. Y. F. Tan, P. L. A, and K. Jagannathan, “A Survey of Risk-Aware Multi-Armed Bandits,” May 12, 2022, _arXiv_: arXiv:2205.05843. doi: 10.48550/arXiv.2205.05843. ↩
- T. Lattimore and C. Szepesvári, _Bandit Algorithms_, 1st ed. Cambridge University Press, 2020. doi: 10.1017/9781108571401. ↩

太强了大佬